Dr hab. Dmytro Zaitsev, prof. WSIiZ

Professor of Computer Science Department, University of Information Technology and Management in Rzeszow, senior member of the ACM and IEEE, recently visiting professor to Université Côte d’Azur, France. In 2017, he was a visiting professor to The University of Tennessee Knoxville, USA on Fulbright scholarship, working in Innovative Computing Laboratory headed by Jack Dongarra. As a result, a joint paper published and software ParAd issued. Dmitry A. Zaitsev developed: theory of linear system clans; small universal Petri and Sleptsov nets in explicit form; generalized neighborhood for cellular automata; theory of infinite Petri nets; algorithm for fuzzy logic function synthesis.

Seminal Turing Award Talk of 2021 Laureate of Turing Award Jack Dongarra to the International Conference for High Performance Computing, Networking, Storage, and Analysis (SC22) sheds new light on the problems of modern supercomputers development. His deep analysis of the supercomputers efficiency implies a conclusion that the architecture of the most powerful computers in the world is not completely adjusted for solving practical tasks in challenging application domains. In this situation, Sleptsov Net Computing looks as a promising approach capable to provide a breakthrough in the issues of modern supercomputers efficiency.

Concept of Sleptsov Net Computing (SNC) has been described in a journal paper [1], historical aspects discussed in a known USA publisher IGI-Global News Room The Highest Standard: Sleptsov Software, on May 23, 2017. Recent paper [2] mathematically proves that any given concurrent algorithm can be specified by a Sleptsov net; it is published by prof. Zaitsev with WSIZ affiliation in one of the best world computer science journals entering CORE A list.

Dr. Jack Dongarra’s contribution to modern computer science and the issues raised in his speech

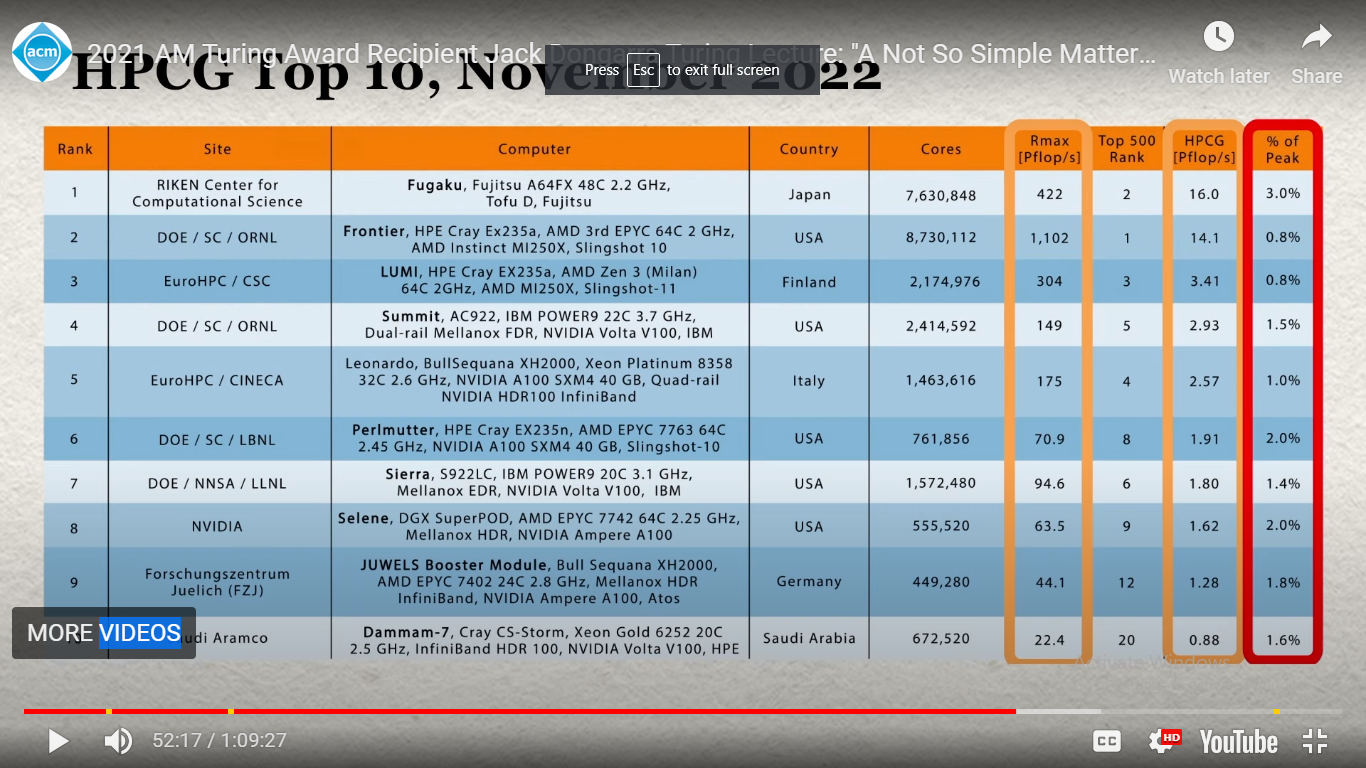
For more than two decades, efficiency of supercomputers has been measured solving big dense random linear systems using LINPACK library. In his Turing Award talk, Jack Dongarra calls LINPACK a yardstick of high performance computing. Using this yardstick, a series of supercomputers, in USA and other countries, has been developed, including the most powerful computer in the world at the present time – Frontier of Oak Ridge Laboratory, USA. Remind that, performance of computers is measured in FLOPS – floating point operations per second, and Frontier breaks exaflops barrier that amounts to ten to the eighteenth power flops. In the final part of his talk, Jack Dongarra reveals recently obtained information on efficiency of the best computers, mentioned in Top500 list, during solving real-life tasks in manifold application domains basically represented by simulators which lead to solving sparse linear systems.

Frontier and many other top computers show efficiency about 0.8% that means Frontier has real performance about ten petaflops instead of an exaflops. Only Japanese computer Fugaku of Fujitsu, occupying recently the second place, reaches 3.0% efficiency.

Indeed, supercomputing is not so simple as cutting up plots of land to measure them with a single yardstick but requires a complex balanced approach of using a mixture of simulators for the top significant application domains. Dense systems provide regular load on processors and communication subsystem filling the cache well to smooth out the processor-memory bottleneck.

Real life tasks, represented by simulators and sparse systems, require irregular communication pattern that is implemented rather well by the Fugaku’s six dimensional torus Tofu D Interconnect. Thus, design of communication subsystems in the form of a multidimensional torus represents a prospective direction of research, studied by prof. Zaitsev and his coauthors using theory of infinite Petri nets.

The computer based on the Sleptova network shows no bottleneck in the processor-memory system and exhibits the highest performance

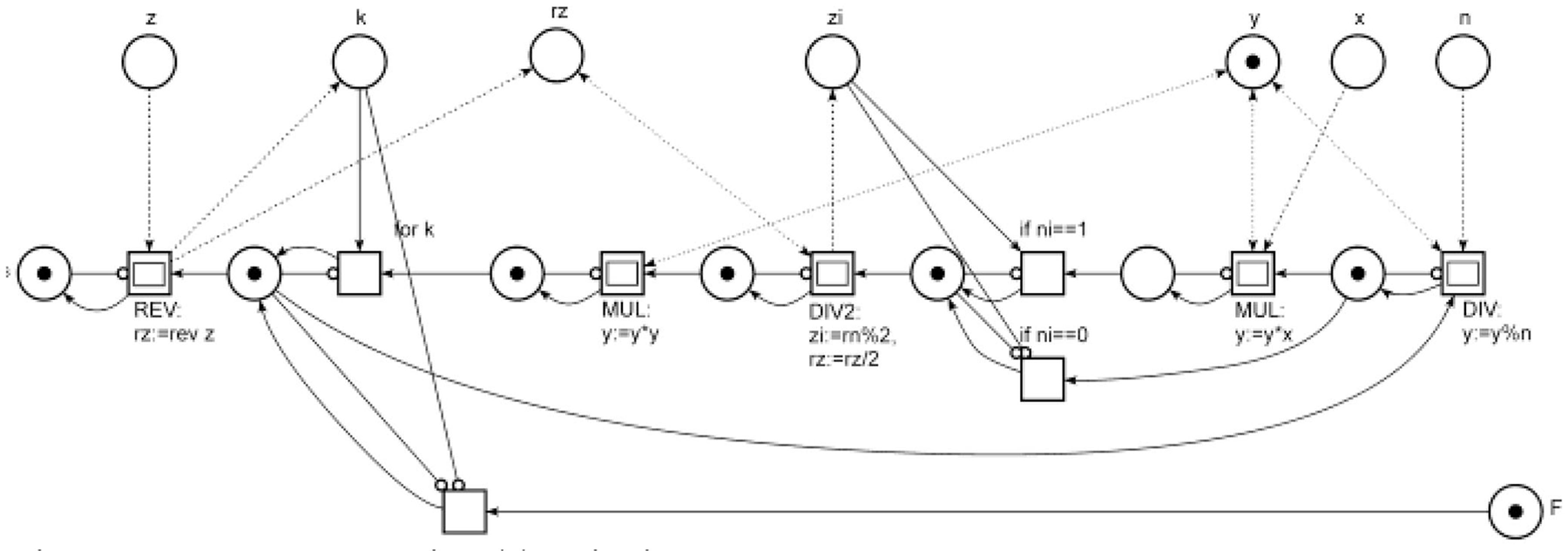
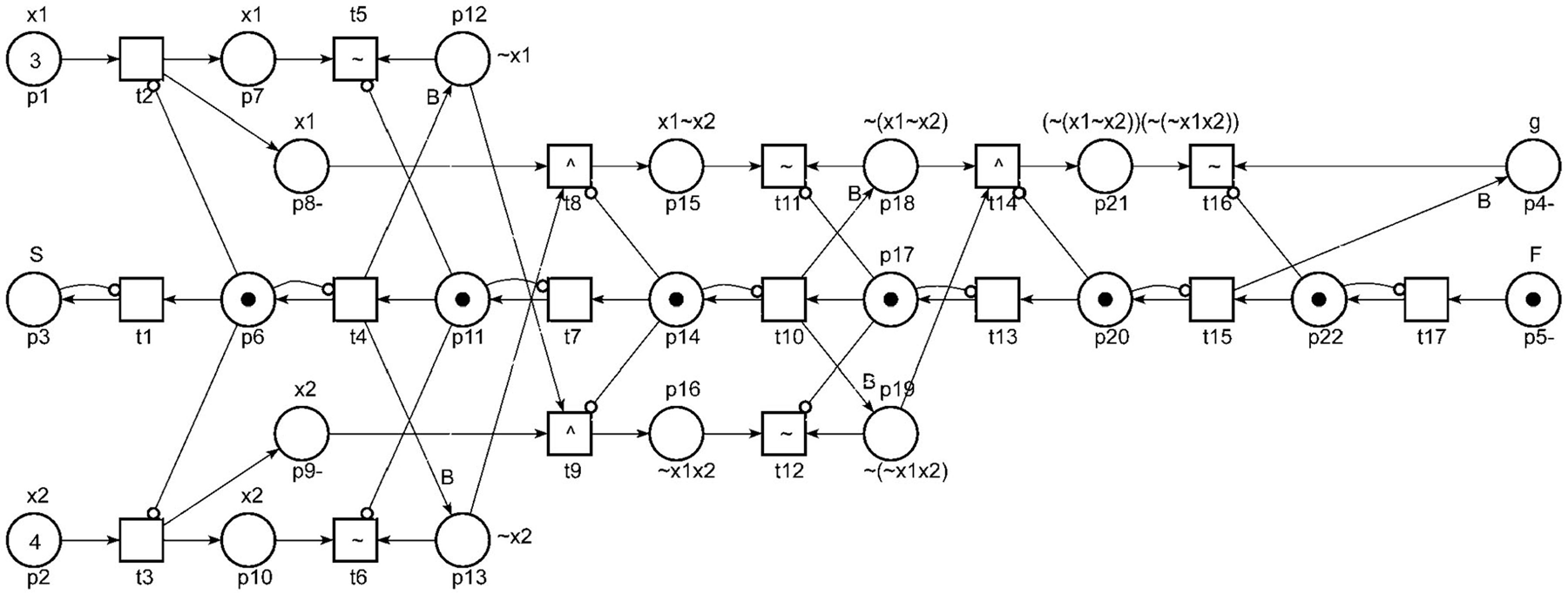
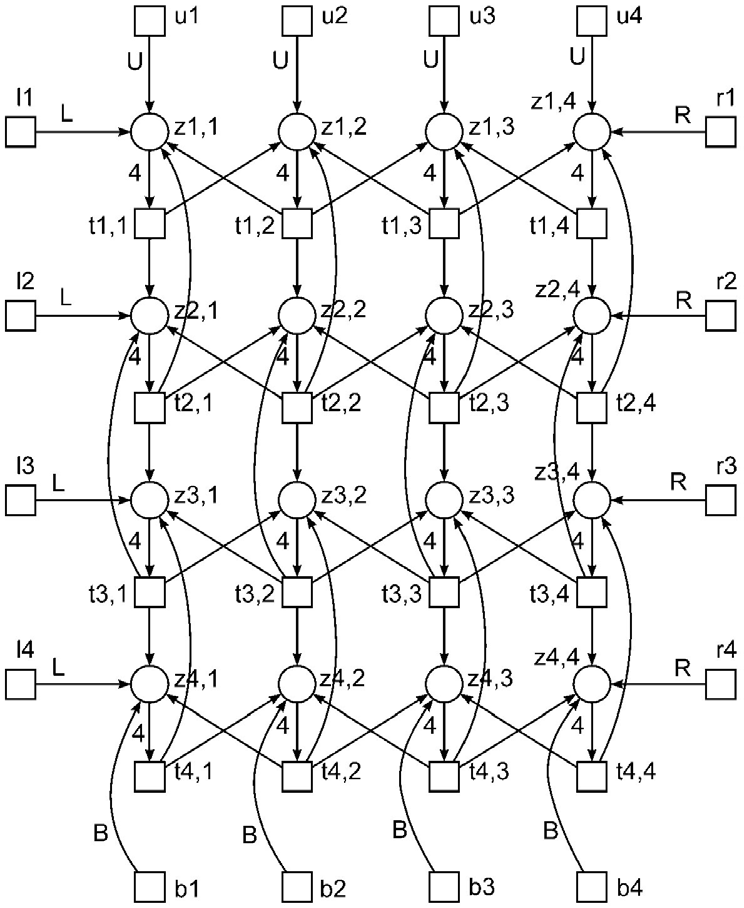
Sleptsov Net Computing goes further; it uses computing memory, represented as two and higher dimension structures, when spatial peculiarities of modeled systems are taken into consideration. Doing computations in memory allows us to get rid of the traditional processor-memory bottleneck problem. Instead of sophisticated conventional architecture to utilize multicore CPUs and GPUs of distributed nodes, for instance with OpenMP-CUDA-MPI set tools, Sleptsov Net Computing offers homogenous concept of a unified graphical language for concurrent programming with very fine granularity of parallel computations. As grown from place-transition net theory, Sleptsov net inherits developed methods to analyses and prove correctness of parallel programs in the process of their model-driven development. Implementation of Sleptsov net processors in the form a matrix of computing memory leads to the nanosecond tack of time of massively parallel computations that means good ability to control hypersonic objects in real-time applications.

Software reliability is a separate issue. Let us imagine that reliability of a bulk of software operating in the world is based on the belief that it does not contain an error or rather contains an error with low probability. The belief is supported by a certain number of successful tests on which a program in question works correctly. Such software is embedded in cars’ and planes’ onboard computers, to make us believe in low probability of an accident, while we prove correctness of concurrent Sleptsov net programs in a formal way.

Below we collected Sleptsov net programs for various application domains:

Recently, master students of prof. Zaitsev implemented software prototypes of a Sleptsov net processor and a compiler-linker of Sleptsov net programs and presented them at an international conference, IEEE publication of their talks is coming soon. We invite students and researchers all over the world to participate development of Sleptsov net computer hardware and programming technology.

We invite also investors to start-up the project of enterprise level implementation of Sleptsov net computing paradigm, including hardware implementation of Sleptsov net processor and computer. To integrate it initially into the conventional infrastructure, we attach it, as an extension device, to a traditional computer, how it was mentioned in Jack Dongarra talk as one of prospective directions for further developing modern architecture of HPC.

Petri nets, Salvitsky and Sleptsov as a continuation of the work of Gilbreth and Gill

Besides, at the present time, an SNC full-scale project background has been well prepared by manifold keynote talks and dedicated lectures as well as with about a dozen of publications, including Special issue Petri/Sleptsov net based technology of programming for parallel, emergent and distributed systems of International Journal of Parallel, Emergent and Distributed Systems.

Recently published online paper [2] shows that we can use Sleptsov net only (without involving other concepts) to specify any computations. It represents a solid theoretical background for homogeneity of SNC.

The paper also gives an impartial historical view of the parallel software schemata development. Firstly, parallel processes schemata appeared in early works of Frank and Lilian Gilbreth dated 1921 and was standardized in 1947. In 1958, Gill started using bipartite directed graphs to specify parallel computations. In 1962, Petri further develops the model of place-transitions nets adding tokens and transition firing rule. Agerwala and Hack extend the model with inhibitor arcs in 70-ties. Salwicki and Sleptsov in 80-ties generated ideas of the maximal parallel and the multiple transition firing, further developed and published in works of Burkhard and Zaitsev. Turing complete place-transition nets represent a perfect graphical language for concurrent computing, though they run exponentially slower compared a Turing machine.

Finally, Sleptsov net mends this flaw running fast and opening prospects for hardware implementation of a homogenous massive parallel supercomputer. The prospective direction is implemented in prototypes awaiting investments for its full-scale implementation. Let us apply at least 10% of wasted 99.2% of investment into modern USA supercomputers (the number taken from Jack Dongarra Turing Award Talk) to SNC implementation project to obtain a new record of real-life efficiency of computations.

Research direction, presented in the blog post, was also digested by ACM Tech News: Sleptsov Net Computing Resolves Modern Supercomputing Problems, The April 21, 2023, edition of ACM TechNews. More info on SNC you cand find HERE.

References

1. Zaitsev D.A. Sleptsov Nets Run Fast, IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2016, Vol. 46, No. 5, 682 – 693
2. Dmitry A. Zaitsev, Strong Sleptsov nets are Turing complete, Information Sciences, Volume 621, 2023, Pages 172-182.

P.S.

During my life I was lucky to find the best teachers, more precisely, I was lucky they, Anatoly Sleptsov in 1988, and Jack Dongarra in 2017, chose me as an apprentice. I learned much on concurrent processes and place-transition nets from Anatoly Sleptsov, then he directed me to practical implementation of our theoretical results at Topaz plant, and Opera-Topaz was born in 1990 before such nets were called a “workflow” and the speed-up principle was called an “exhaustive use of rule”. Jack Dongarra introduced me to the miraculous world of supercomputers and directed me through the process of my clan theory implementation on modern parallel and distributed architecture, joint software issued, join papers published. I devoted my ode to Jack Dongarra and I like to believe that our joint work switched compass of his research a bit more towards sparse computations.

Artykuł w języku polskim znajduje się TUTAJ.