Mgr inż. Paweł Klimasara

Asystent w Katedrze Kognitywistyki i Modelowania Matematycznego Wyższej Szkoły Informatyki i Zarządzania w Rzeszowie. Magister fizyki (Uniwersytet Śląski) oraz inżynier matematyki stosowanej z informatyką (Politechnika Śląska). Jego zainteresowania naukowe koncentrują się na fizyce matematycznej i jej związkach z podstawami matematyki, w szczególności na wykorzystaniu narzędzi logiki matematycznej oraz teorii mnogości do badań w obrębie mechaniki kwantowej i kosmologii. Ponadto zajmuje się modelowaniem matematycznym w naukach biologicznych, opartym o hybrydowe procesy stochastyczne.

Większość osób z pojęciem nieskończoności spotyka się głównie w szkole na lekcjach matematyki – jednak jej samej nie poświęca się na nich wiele uwagi. Na zajęciach szkicujemy linie proste, a raczej ich mały wycinek, wierząc, że dalej ciągną się one „w nieskończoność”, albo korzystamy z liczb, których jest „nieskończenie wiele” – cokolwiek to znaczy.

Matematycy o nieskończoności (a nawet o nieskończonościach – bo istnieje ich wiele rodzajów*) wiedzą już całkiem sporo, ale jeśli nie odbędziemy kursu teorii mnogości, prawdopodobnie nigdy się z nimi nie zetkniemy. Na szczęście nie trzeba studiować matematyki, żeby czegoś ciekawego na temat nieskończoności się dowiedzieć – już prosty przykład liczb naturalnych skrywa w sobie więcej, niż mogłoby się wydawać.

Przypomnijmy, że liczby naturalne reprezentują nasz podstawowy sposób liczenia: jeśli na przykład chcemy się dowiedzieć, ile osób czeka w kolejce do sklepu, to możemy namierzyć pierwszą osobę i później kolejno widzimy drugą, trzecią, czwartą i tak aż do końca kolejki. Jeśli ostatnia osoba była ósma, to łącznie czeka oczywiście osiem osób. Cały proces bez trudu przeprowadzi już małe dziecko, być może wspomagając się „liczeniem na palcach” – które samo w sobie reprezentuje ten sam sposób liczenia. Jeśli osób byłoby dużo więcej – na przykład sto tysięcy – to proces liczenia potrwa znacznie dłużej, ale nietrudno sobie wyobrazić, że będzie przebiegał identycznie i finalnie się wszystkich tych osób „doliczymy”.

Liczby naturalne są matematycznym przedstawieniem możliwych do uzyskania w ten sposób wyników – innymi słowy reprezentują dowolną skończoną liczbę elementów. Nieważne jednak, jak dużą liczbę będziemy rozważać, zawsze możemy do niej dodać jeden i w efekcie uzyskać inną – jeszcze większą. Często skrótowo zapisujemy zbiór wszystkich liczby naturalnych jako {1, 2, 3, 4, 5, …}. W tym zapisie trzy kropki „skrywają” wszystkie kolejne liczby naturalne – ustawione w naturalnej kolejności, gdzie każda kolejna jest o jeden większa od poprzedniej. Ponieważ sam proces wskazywania liczby kolejnej jest dla nas intuicyjny, to wprowadzenie takiego nieskończonego zbioru nie budzi większych wątpliwości. Jednak zaakceptowanie już nawet takiej „prostej” nieskończoności (nazywanej przeliczalną) umożliwia wiele operacji, które …przeczą ludzkiej intuicji.

Hotel Hilberta – rozważania na przykładzie

Popularną metodą obrazowego przedstawienia nieintuicyjnych właściwości nieskończoności jest eksperyment myślowy znany jako „Hotel Hilberta” (Hilbert’s Paradox of the Grand Hotel) – od nazwiska jego autora, niemieckiego matematyka Davida Hilberta. Wyobraźmy sobie hotel, który ma nieskończoną liczbę pokoi, a w nich nieskończoną liczbę gości –  dla uproszczenia po jednej osobie na każdy pokój. Mamy więc gościa w pokoju pierwszym, innego gościa w pokoju drugim, kolejną osobę w pokoju trzecim i tak dalej – a więc dla każdej liczby naturalnej mamy zajęty pokój o danym numerze. Gdyby do hotelu przyszedł nowy klient, to w sytuacji skończonej liczby pokoi sprawa byłaby prosta – wszystkie pokoje są zajęte, więc nie możemy go przyjąć. Jednak – mimo tego, że w hotelu Hilberta każdy pokój ma już mieszkańca – bez problemu znajdziemy miejsce dla nowego gościa. Potrzebujemy do tego niewielkiej pomocy aktualnych mieszkańców, mianowicie prosimy osobę z pierwszego pokoju, aby przeniosła się do pokoju drugiego, osobę z pokoju numer dwa, żeby przeniosła się do pokoju numer trzy, z kolei osobę, która do tej pory była w pokoju numer trzy, aby przeszła do czwartego i tak dalej – prosimy każdego z gości o przeniesienie się do pokoju o numerze o jeden większym. Tym sposobem nikogo nie wyrzuciliśmy ani nie wymusiliśmy na nim współlokatora – każdy dostał nowy pokój po „poprzedniku”. Co ważniejsze: nikt nie pojawił się w pokoju numer jeden, bo każdy poszedł do pokoju o numerze większym. Dzięki temu bez problemu zakwaterujemy w jedynce nowego gościa.

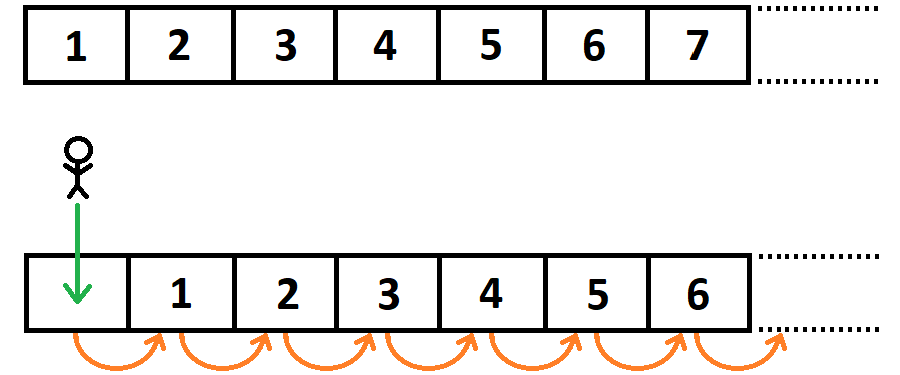
Analogicznie możemy się zachować dla dowolnej skończonej liczby gości. Dla przykładu załóżmy, że w recepcji pojawił się nie jeden, a szesnastu nowych klientów. Pomimo faktu, że wszystkie pokoje są zajęte, również znajdziemy miejsca dla nowych gości. Podobnie jak poprzednio poprosimy aktualnych lokatorów o zmianę pokoju – tym razem o przejście nie do pokoju kolejnego, a do takiego, który ma numer o szesnaście większy. Czyli osoba z pierwszego pokoju wyląduje w pokoju z numerem 1+16=17, mieszkaniec z pokoju numer 2 przeniesie się do pokoju numer 18, gość z trójki znajdzie się w pokoju z numerem 19 i tak dalej. Tym sposobem wszyscy aktualni goście pozostaną zakwaterowani w nowych pokojach, a my mamy zwolnione miejsca w pokojach o numerach od 1 do 16 – czyli w sam raz dla nowo przybyłej grupy osób.

Kolejni goście w hotelu Hilberta

Wiemy już, jak powinien zachować się recepcjonista, aby pomieścić dowolnie dużą (ale skończoną) liczbę nowych gości, nawet w sytuacji przepełnionego hotelu. Rozważmy teraz równie hipotetyczną sytuację co sam hotel – gdy w budynku pojawia się nieskończona liczba nowych klientów. Gdybyśmy mimo wszystko chcieli ich zakwaterować, to nasza dotychczasowa taktyka nie zadziała: przeniesienie osoby o „nieskończoną liczbę” pokoi nie jest odpowiednio zdefiniowanym działaniem – nie wiemy, do którego konkretnie pokoju miałaby ona trafić.

Mimo to poradzimy sobie i z tym zadaniem. Jedną z metod rozwiązania tej sytuacji jest poproszenie każdego z aktualnych gości o przeniesienie się do pokoju o numerze dwa razy większym. Osoba z pierwszego pokoju trafiłaby do drugiego, osoba z dwójki przeniosłaby się do pokoju numer 4, mieszkaniec pokoju numer 3 wylądowałby w pokoju numer 6, gość spod czwórki zostałby mieszkańcem 8 i tak dalej. Tym sposobem mamy nowy pokój dla każdego dotychczasowego klienta, a wszystkie pokoje, których numer nie jest dwukrotnością innej liczby (a więc te o numerach nieparzystych), są teraz puste. I, podobnie jak samych liczb nieparzystych, jest ich nieskończenie wiele.

Wobec tego pierwszego nowego gościa możemy zakwaterować w pokoju o pierwszym numerze nieparzystym (jedynce), drugiego możemy wysłać do pokoju o drugim numerze nieparzystym (do trójki) i kolejnych do pokoi u numerach 5, 7, 9, 11, … W ten sposób każdy nowy gość trafi do jednego z pustych pokoi i ponownie uda nam się wszystkich pomieścić.

Rozważmy teraz sytuację, w której przed hotelem pojawiają się dwa autobusy, a w każdym z nich – nieskończenie wielu nowych klientów. Jeśli miejsca w autobusach są ponumerowane liczbami naturalnymi – jak pokoje w naszym hotelu – to i tym razem damy radę przyjąć wszystkich. Jednym z prostszych sposobów będzie podstawienie trzeciego autobusu i poproszenie dotychczasowych gości hotelu o tymczasowe zajęcie w nim miejsca o numerze odpowiadającym numerowi ich pokoju. Dzięki temu mamy trzy autobusy z nieskończoną liczbą osób w środku każdego z nich oraz pusty hotel Hilberta. Teraz możemy wszystkich rozlokować, na przykład przypisując do kolejnych pokoi (oczywiście zaczynając od pierwszego): osobę na miejscu numer 1 z pierwszego autobusu, osobę z miejsca numer 1 z drugiego autobusu, siedzącego pod numerem 1 w trzecim autobusie, później klientów siedzących na drugim miejscu kolejno w każdym z autobusów, następnie siedzących na trzecich miejscach i tak dalej. Dzięki temu każdy trafi do innego pokoju i dla wszystkich starczy miejsca. Ponownie możemy bez trudu uogólnić taką strategię na większą (ale skończoną) liczbę autobusów z nieskończoną liczbą gości każdy. Dla przykładu załóżmy, że podjeżdża 999 takich autobusów. Podstawiamy tysięczny autobus dla dotychczasowych gości i mamy 1000 pojazdów pełnych ludzi oraz pusty hotel. Osoby z pierwszego miejsca kolejno z każdego z autobusów umieścimy w pokojach o numerach od 1 do 1000, osoby z miejsc drugich kolejno w pokojach numerowanych od 1001 do 2000 i tak dalej.

Nieskończenie wiele autobusów pod hotelem Hilberta

Możemy sytuację jeszcze bardziej skomplikować: powiedzmy, że pod hotel podjeżdża nieskończenie wiele autobusów i w każdym z nich siedzi nieskończenie wielu potencjalnych klientów. I to się uda, chociaż metody na przyjęcie wszystkich gości w takim wypadku wymagają od nas troszkę większej wiedzy matematycznej.

Przydatnymi okażą się tak zwane liczby pierwsze, czyli te spośród liczb naturalnych (poza jedynką), które mają tylko dwa dzielniki – samą siebie oraz liczbę jeden. Przykładowo 2 jest liczbą pierwszą, bo dzieli się tylko przez 2 i przez 1, podobnie 3 jest liczbą pierwszą, bo jej jedynymi dzielnikami jest 3 oraz 1. Ale już liczba 4 liczbą pierwszą nie jest, bo oprócz 4 i 1 dzieli się ona również przez liczbę 2. Kolejna liczba, czyli 5, znowu jest liczbą pierwszą, bo nie ma innych dzielników niż 5 i 1, z kolei 6 znowu nie jest pierwsza, bo dzielą ją 2 i 3. Kilka kolejnych liczb pierwszych prezentuje się w ten sposób: 2, 3, 5, 7, 11, 13, 17, 19, … Co dla nas ważne, można udowodnić, że dla dowolnej takiej liczby istnieje liczba pierwsza od niej większa. Stąd zbiór liczb pierwszych jest nieskończony i możemy mówić o pierwszej z kolei liczbie pierwszej (czyli dwójce), drugiej liczbie pierwszej (trójce), trzeciej liczbie pierwszej (piątce) i tak dalej – mamy je wtedy ponumerowane jak pokoje w naszym hotelu.

Drugim podstawowym faktem teorii liczb, który nam się przyda, jest możliwość przedstawienia każdej liczby naturalnej (poza jedynką) jako iloczynu potęg liczb pierwszych. Na przykład liczbę 8 możemy zapisać jako, czyli 2³ (dwa do potęgi trzeciej), natomiast liczbę 630 możemy przedstawić jako wynik mnożenia , czyli 2¹3²5¹7¹ (dwa do potęgi pierwszej razy trzy do potęgi drugiej razy pięć do potęgi pierwszej razy siedem do potęgi pierwszej). Każda rozważana liczba ma inną reprezentację tego typu, lub – w drugą stronę – jeżeli mówimy o liczbach postaci na przykład 2^a3^b, czyli liczba 2 do pewnej potęgi a razy liczba 3 do pewnej potęgi b, to jeśli chociaż jedna spośród tych liczb a, b się zmieni, uzyskamy inną liczbę. To jest wybierając każdorazowo inne naturalne a i b, żadna z liczb się nie powtórzy.

Wykorzystamy ten fakt do rozwiązania nowej sytuacji w hotelu. Przypomnijmy, że przyjeżdża nieskończona liczba autobusów z nieskończoną liczbą nowych gości w każdym z nich, gdzie każdy z pojazdów i siedzeń w nich są numerowane liczbami naturalnymi. Najpierw wykorzystamy podobny trik jak na początku z dokwaterowaniem jednej osoby. Poprosimy najpierw, aby pasażerowie pierwszego autobusu przesiedli się na takie same miejsca w autobusie drugim, jadących autobusem drugim, aby przesiedli się do autobusu trzeciego, pasażerów trzeciego o przejście do czwartego i tak dalej. Dzięki temu wszyscy zmienią autobus, dla nikogo nie zabraknie w nich miejsca i – przede wszystkim – pierwszy autobus będzie pusty.

Wobec tego ponownie poprosimy aktualnych gości hotelowych o tymczasowe przeniesienie się do niego, zajmując miejsca o tych samych numerach co ich pokój. Po tej operacji sytuacja zmienia się na nieskończenie wiele autobusów z nieskończoną liczbą pasażerów każdy i pusty hotel Hilberta. Wystarczy przypisać wszystkich do pokoi w taki sposób, żeby było wiadomo, do którego ma się udać każdy z nich oraz aby nikt nie trafił do pokoju już zajętego.

Wykorzystamy przypomnianą własność, że liczba 2^a3^b jest inna dla różnych a i b. Wobec tego wystarczy, że każdy z pasażerów uda się do pokoju o numerze 2^a3^b, gdzie za liczbę a podstawi numer swojego autobusu, a za liczbę b numer swojego miejsca w autobusie. Przykładowo pasażer autobusu czwartego siedzący na miejscu numer pięć trafi do pokoju o numerze 2⁴3⁵ =222233333=3888. Ponieważ każda z osób albo jedzie innym autobusem, albo siedzi na innym miejscu w tym samym busie, to dla każdej z osób co najmniej jedna z liczb a i b się różni – a więc różni się też numer pokoju, do którego ma się udać.

Tym samym znowu udało nam się wszystkich pomieścić, a nawet więcej – po udaniu się wszystkich do swoich nowych apartamentów ponownie nieskończenie wiele z pokoi pozostanie pustych! Przykładowo do pokoju numer pięć nikt nie trafi, bo nie da się tej liczby przedstawić jako iloczyn potęg dwójki i trójki. Podobnie nikt nie trafi do pokoi o numerach 7, 11, tych odpowiadających kolejnym liczbom pierwszym, wszystkich pokoi będących ich potęgami i tak dalej. Podobnie możemy poradzić sobie z sytuacjami, w których dołożymy skończenie wiele kolejnych „warstw nieskończoności”: przykładowo wyobraźmy sobie, że hotel jest nad morzem i do jego portu przybija nieskończenie wiele promów, a na każdym z nich stoi nieskończona liczba autobusów z nieskończoną liczbą pasażerów. Podobnie jak ostatnio wykorzystaliśmy liczby o postaci iloczynu potęgi dwójki i potęgi trójki, teraz moglibyśmy wysłać każdego z pasażerów do pokoju o numerze 2^{numer promu}3^{numer autobusu}5^{numer siedzenia} i podobnie można by dokładać kolejne warstwy jako potęgi kolejnych liczb pierwszych. Mało tego – każdorazowo pozostawimy nieskończenie wiele pustych pokoi…

* tak zwanych liczb pozaskończonych