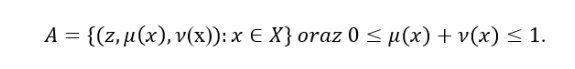Adiunkt w Katedrze Kognitywistyki i Modelowania Matematycznego Wyższej Szkoły Informatyki i Zarządzania w Rzeszowie. Prowadzi badania w dziedzinie relacyjnych układów równań oraz rozmytych zbiorów zbalansowanych oraz ich zastosowań. Jej dorobek naukowy obejmuje artykuły naukowe oraz wystąpienia na konferencjach naukowych. Ponadto, udziela się również w zakresie popularyzacji nauczania informatyki dzieci i młodzieży. Prywatnie uwielbia spędzać czas z rodziną na wycieczkach i wyprawach turystyczno-przyrodniczych oraz z mężem przy dobrej kawie.
Prawda, fałsz oraz to, co znajduje się pomiędzy…
Od wieków ludzie zastanawiają się, co jest prawdą a co fałszem. W klasycznej logice formalnej stwierdzenie, co do którego możemy orzec, że jest ono prawdziwe lub fałszywe, nazywamy zdaniem. Choć uczciwie powiedziawszy już Platon poddał myśl, że musi istnieć coś trzeciego pomiędzy prawdą i fałszem.
W latach trzydziestych poprzedniego wieku to polski naukowiec prof. Jan Łukasiewicz zauważył ten fakt wprost i wprowadził do logicznych rozważań nad prawdziwością zdania wartość 1/2, czyli odpowiednik potocznego stwierdzenia „trudno powiedzieć”. Jego dalsze rozważania doprowadziły go do napisania pracy, w której wprowadza wartości prawdziwości z przedziału [0, 1], czyli upraszczając do stopniowania poziomu prawdziwości zdania (od 0 – czyli zdania, co do którego nie ma wątpliwości, że jest fałszywe, po 1 – oznaczające zdanie na pewno prawdziwe, zaś wartości pomiędzy oznaczają tylko częściową prawdziwość. Wrócimy do tego w dalszej części tego opisu).
Czy teoria Łukasiewicza oznacza, że prawda się rozmywa? Nie nam – matematykom – dyskutować na temat, czy to prawda się rozmywa, czy raczej nasze wahania dotyczące opisu rzeczywistości łatwiej opisywać. Ale faktem jest, że prace prof. Jana Łukasiewicza stały się punktem, gdzie Logika Arystotelesowska (zero-jedynkowa) zaczęła robić miejsce dla Logiki Rozmytej.
Kolor niebieski w roli głównej czyli to wszystko nie jest takie oczywiste…
Zobaczmy trzy ilustracje i odpowiedzmy na pytanie: Czy zaznaczony przedmiot jest niebieski? Sytuacja pierwsza. Pytanie wydaje się proste. Tak, zaznaczona kredka jest niebieska.
Źródło: https://bagobag.pl/pins-wpinka-przypinka-kolorowe-kredki-colors-crayons
Sytuacja druga – tutaj już pewności nie mamy, prawda? Kredka trochę jest niebieska, ale trochę
także zielona. Czyli w jakim stopniu jest ona niebieska, może 4/10 (czyli w stopniu 0,4)?

Źródło: https://blog.fiszki.pl/jezyki/hiszpanski/kolory-po-hiszpansku/
Sytuacja trzecia. Tutaj także musimy powiedzieć, że jest to kolor niebieski, ale w jakim w stopniu… ? Proszę sam/sama dokonaj oceny!

Źródło: https://mojeprojektowanie.pl/kod-koloru-jak-sprawdzic-kolor/
Zbiory i pojęcia rozmyte
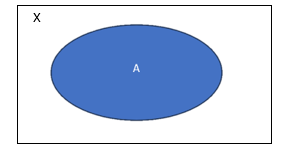
W związku z tym nowym podejściem do logiki i potrzebą analizy (dość niejednoznacznego) świata rzeczywistego i na koncept zbioru spojrzano nieco inaczej. Dotychczas, w matematyce rozważano jedynie wszystkim znane klasyczne zbiory (w rozumieniu, że coś należy do zbioru lub nie – zob. rys. 1).
Rys.: 1 Zbiór A w przestrzeni X.
Zatem zbiór wartości funkcji charakterystycznej klasycznego zbioru ma tylko dwie wartości 1 –element należy do zbioru oraz 0 – element nie należy do zbioru:
Jednak ten tak elegancko poukładany i zaksjomatyzowany świat zbiorów (zobacz prace Russella, Zermelo, Fraenkla), obdarty z wszelkich paradoksów i antynomii postaci: Ciocia lubi osoby, które siebie nie lubią. Czy ciocia siebie lubi, czy nie? i innych, znów musi zmierzyć się z nowymi wyzwaniami.
Jednym z nich jest pytanie, czy elementy mogą należeć do zbioru częściowo? Na bazie tego pytania powstała koncepcja zbiorów rozmytych, wprowadzona przez prof. Lotfi A. Zadeha w 1965 roku (Zadeh L. , 1965). Funkcja przynależności μ:X→[0,1] określa dla każdego elementu ze zbioru X stopień jego przynależności do niego. Wartości funkcji przynależności są z przedziału [0, 1], gdzie 0 oznacza brak przynależności do zbioru, zaś 1 – pełną przynależność do zbioru, zaś wartości z przedziału (0,1) oznaczają przynależność do zbioru w pewnym stopniu. Zadeh w swojej pracy zaczął rozważania od podania przykładów „pojęć rozmytych”, postarajmy się i my podać kilka: wysoki człowiek, piękny obraz, mądry student, ciekawy wykład, głośna maszyna itd.
Aby dobrze to zilustrować zadajmy sobie „proste” pytanie: Jaki wzrost powinna mieć osoba określana mianem wysokiej? 180 cm? Ok, czyli w takim razie osoba mająca 179,6 cm nie jest już wysoka. A co z osobą liczącą 176 cm? Osoba mająca 180 cm i więcej należy do zbioru osób wysokich w stopniu 1, ale jak osoba ma „niewiele” poniżej 180 cm, to czy jest wysoka w stopniu 0,95, albo 0,8? I czy osoba mająca 165 cm jest wysoka w stopniu 0,09? A ta mająca 159 nie jest wysoka, tylko już niska? „Proste” pytania okazują się wcale nie takie proste!
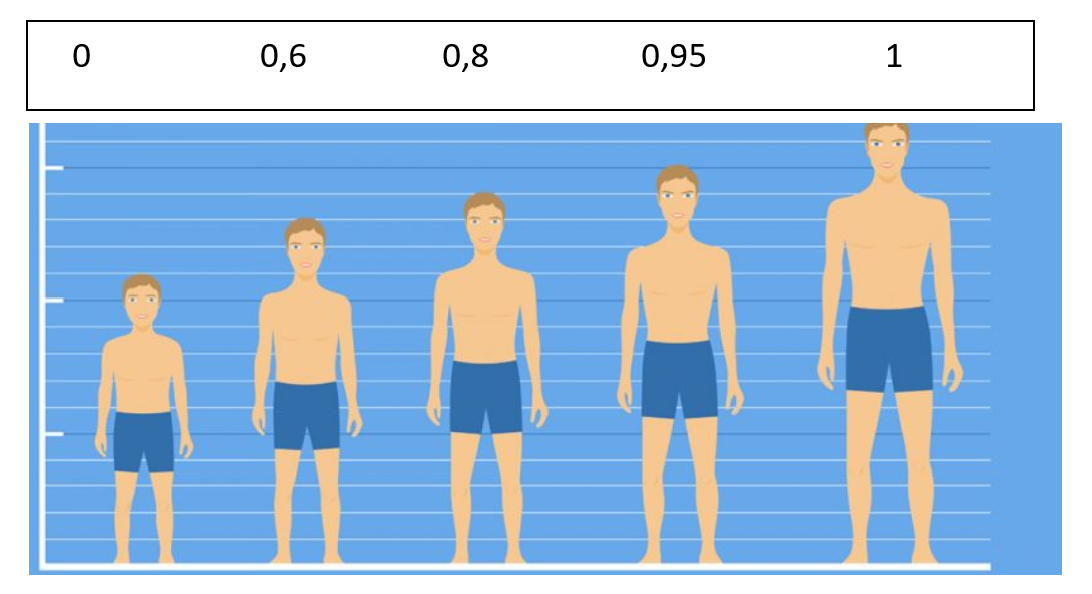
Źródło: https://jakurosnac.pl/wiek-ma-znaczenie-w-zwiekszaniu-wzrostu/
Ewolucja zbiorów rozmytych
Podsumujmy więc: dla zbiorów rozmytych opracowano solidne postawy teoretyczne, dzięki czemu przez długi czas służyły one do reprezentacji wiedzy nieprecyzyjnej. Dzięki nim możliwe było przeniesienie na modele matematyczne zjawisk i pojęć niejednoznacznych i nieprecyzyjnych, a naturalnie używanych w życiu codziennym (oraz wykorzystywanych w naturalnej komunikacji międzyludzkiej), takich jak mądry człowiek, ładny dom, posprzątany pokój, wysokie wynagrodzenie, itp. Niemniej jednak koncepcja ta ewaluowała, gdyż liczni naukowcy – próbując opisywać zjawiska naturalne – z rozmysłem dokładali kolejne rozszerzenia zbiorów rozmytych. Pierwsze z nich pojawiło się już w 1967. Wówczas prof. Joseph A. Goguen przeniósł pojęcie zbiorów rozmytych na kraty, czyli wprowadził L-fuzzy sety (Goguen, 1967). Dalej, w 1975 roku, Zadeh wprowadził przedziałowe zbiory rozmyte (Zadeh L. A., 1975). Funkcja przynależności przedziałowego zbioru rozmytego odwzorowuje zbiór obiektów z przestrzeni U na zbiór wszystkich domkniętych przedziałów zawartych w przedziale [0, 1]. Ten typ zbiorów ma zastosowanie, gdy stopień przynależności do zbioru nie może zostać dokładnie określony, czyli tyczy on informacji niepewnej.
W 1986 roku prof. Krassimir Atanassov wprowadził pojęcie intuitionistycznych zbiorów rozmytych rozważając funkcje przynależności i nie-przynależności (zobacz: (Atanassov K. , 1999), (Atanassov K. T., 1986)), mające postać:
Różnica pomiędzy wartościami funkcji przynależności i nie-przynależności nazywa się stopniem niepewności Π(x)=μ(x)-ν(x). W ten sposób Atanassov zauważył potrzebę rozważania informacji pozytywnej i negatywnej. Jednocześnie wprowadzenie stopnia niepewności przy opisie elementów zbioru daje możliwość odzwierciedlenia ludzkiego sposobu podejmowania decyzji, wyrażania opinii czy opisywania obserwowanego świata.
Koncepcja przekazywania informacji negatywnej jako wartości z przedziału [-1, 0] stanowi nowość w bipolar-valued fuzzy sets (Lee, 2000) . Ta koncepcja jest rozszerzeniem intuitionistycznych zbiorów rozmytych. Precyzując, mamy równocześnie wartości funkcji nie-przynależności są z przedziału [-1,0] oraz funkcji przynależności z przedziału [0, 1].
Niektóre dane nie mają takiej dwojakiej postaci. Jasno charakteryzują, czy element należy do zbioru czy też nie (i w jakim stopniu). Dobrym przykładem są często przeprowadzone badania ankietowe zawierające tylko informację postaci: należy do zbioru w pewnym stopniu, trudno powiedzieć, nie należy do zbioru w pewnym stopniu. Zatem nie jako konkurencję dla rozmytych zbiorów intuitionistycznych, ale jako odpowiedź na takie zapotrzebowanie, powstały rozmyte zbiory zbalansowane.
Ponadto należy zwrócić uwagę, że człowiek często podejmując decyzje określa, jak bardzo coś mu się podoba lub nie. Wiele sytuacji opisywanych przez nauki społeczne, marketingowe, finansowe oraz diagnostyczne jawnie poruszają problem niedoboru i nadmiaru. W niektórych modelach 0 (rozważane w zbiorach rozmytych jako brak przynależności do zbioru) nie niesie ze sobą ani informacji pozytywnej ani negatywnej. Natomiast stany nadmiarowości i niedoboru przekazują do kreowanego modelu konkretne zabarwienie informacyjne.
W 2006 roku prof. Władysław Homenda wprowadził zrównoważone zbiory rozmyte. Koncepcja ta spowodowała rozszerzenie pierwotnej koncepcji zbiorów rozmytych z przedziału [0, 1] na [-1, 1] (zob. Rys. 2).
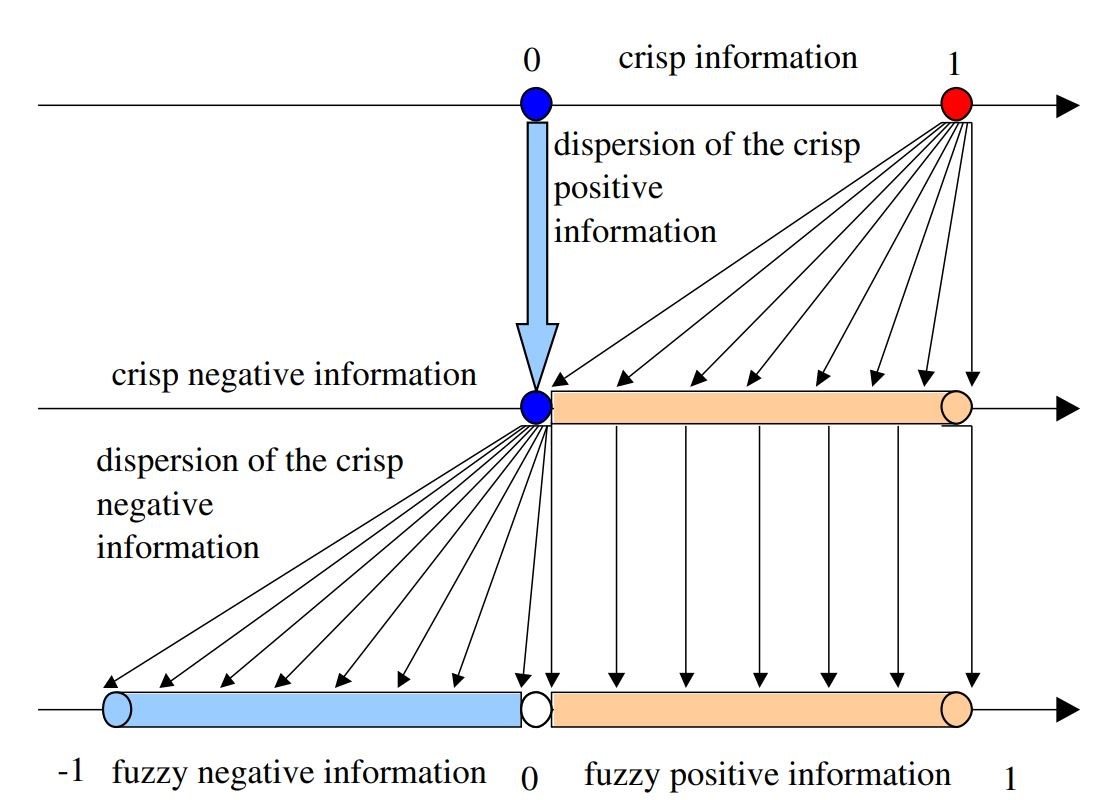
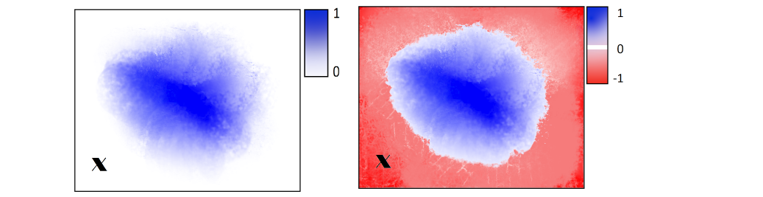
Na Rys.3 widać różnice pomiędzy zbiorami rozmytymi, a rozmytymi zbiorami zbalansowanymi.
Rys. 3: Zbiory rozmyte (po lewej), rozmyte zbiory zbalansowane (po prawej), (Matusiewicz & Homenda 2023).
W zbiorach rozmytych informacja negatywna (oznaczająca „brak”) rozszerza się od wartości 0 do przedziału [-1,0].
Przykłady rozmytych zbiorów zbalansowanych
Do dobrego zrozumienia, czym są zbalansowane zbiory rozmyte, dobrze nadają się wszelkie rzeczy, które mają przeciwieństwa. Na przykład pytanie o to, czy firma ma dobrą kondycję finansową, możemy odpowiedzieć „zero – jedynkowo”: TAK lub NIE.
W przypadku zbiorów rozmytych podamy stopień, jak dobą kondycję finansową ma rozważana firma, czyli od zero – oznaczającego kondycja firmy nie jest dobra, po określając stopień przynależności między zero a jeden. Gdzie 0,1 oznacza, że nie jest najlepiej, ale firma „daje radę”, 0,7 oznacza, że jest dobrze, ale może być lepiej, jeden – jest całkiem dobrze.
W przypadku rozmytych zbiorów zbalansowanych możemy podać stopień, jak bardzo nie jest dobrze. Tak dla przykładu -1 oznacza, że jest całkiem źle. -0,5 jest źle, ale może być gorzej itd.
Innym przykładem są dane i oceny medyczne. Zacznijmy od zilustrowania zapytania, czy dana osoba ma nadwagę:
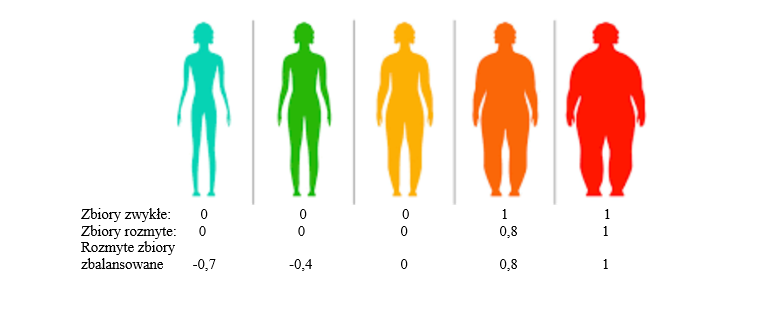
Źródło: https://szpital.siedlce.pl/tiny_files/dietetyka/13.pdf
Oczywiście funkcja (metoda), na podstawie której wyznaczamy stopień przynależenia i nieprzynależenia do zbiorów, mogą być różne. Przykładowo, człowiek podejmując decyzję inaczej to robi rozważając pozytywne i negatywne czynniki.
Gdybyśmy sięgnęli głębiej w nauki społeczne (w tym w Teorię Perspektywy) dowiedzielibyśmy się, że na przykład zadowolenie człowieka rośnie znacznie wolniej pod wpływem pozytywnych bodźców niż spada pod wpływem negatywnych bodźców (przynajmniej w I fazie eksperymentu).
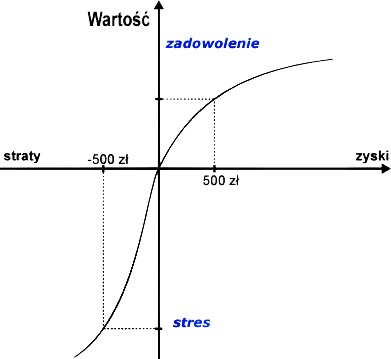
Źródło: https://blogi.bossa.pl/2008/08/31/poziom-stresu-i-zadowolenia/
Nad tematem rozmytych zbiorów zbalansowanych, operatorów zbiorów rozmytych, aplikacyjności tychże zbiorów w opisie i analizie świata rzeczywistego pochyla się również autorka tego wpisu.
Bibliografia:
Atanassov, K. (1999). Intuitionistic fuzzy sets. Springer-Verlag.
Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems 20(1), 87-96.
Goguen, J. (1967). L-fuzzy sets. Journal of Mathematical Analysis and Applications 18(1), 145-174.
Homenda, W. (2006). Balanced fuzzy sets. Information Sciences, 2467 – 2506.
Lee, K.-M. (2000). Bipolar-valued fuzzy sets and their basic operations. Proceedings of the International Conference, (pp. 307–317). Bangkok, Thailand.
Li, J., & Wen, Y. (2013). Decision Making Model Based on Fuzzy Relation Equations Constraints and Its Algorithm. Ninth International Conference on Computational Intelligence and Security, IEEE Computer Society, (pp. 334-338 ). Washington.
Matusiewicz, Z., & Homenda, W. (2023). Balanced fuzzy operations. IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), (pp. 1-8). Incheon, Korea.
Zadeh, L. (1965). Fuzzy sets. Information and Control 8,, 338-353.
Zadeh, L. A. (1975). The concept of a linguistic variable and its application to approximate reasoning – I. Information Sciences 8(3), 199–249.